Parameterize a Curve
What Does It Mean: “Path Parametrized by 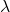 “?
“?
A path parametrized by ![]() is a way of describing a curve through space by using a single variable,
is a way of describing a curve through space by using a single variable, ![]() , to trace the position along the path.
, to trace the position along the path.
🔁 The Idea
You have a curve, say, a person walking on a sphere from the equator to the pole. Instead of describing the path just as a set of points ![]() , we describe it as a function of a parameter:
, we describe it as a function of a parameter:
![]()
This means:
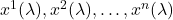 give the coordinates of a point on the path as
give the coordinates of a point on the path as 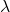 changes.
changes.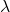 might represent time, arc length, or an abstract index.
might represent time, arc length, or an abstract index.
🧮 Why Parametrize?
Parametrizing a path lets us:
- Take derivatives along the path:
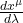 is the tangent vector.
is the tangent vector. - Track how things like vectors
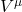 change along the path.
change along the path. - Write transport equations like
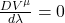 .
.
🧭 Analogy: Driving on a Road
– The road is the path.
– ![]() is your odometer reading (distance traveled).
is your odometer reading (distance traveled).
– ![]() tells you your location at each point.
tells you your location at each point.
– ![]() gives your direction of motion.
gives your direction of motion.
🌀 A Math Example
Let’s say you move in a circle:
![]()
Then you’re moving along a circle, and ![]() is the angle — a natural parameter for this motion.
is the angle — a natural parameter for this motion.
💡 Summary
When we say “a path parametrized by ![]() ,” we mean:
,” we mean:
“Here’s a curve through space, and we’ve assigned a smooth way to move along it — so we can differentiate, transport vectors, and do math.”