Nowhere Differentiable Functions and Integration of such functions
Nowhere Differentiable Functions
Nowhere differentiable functions are functions that are continuous everywhere but do not have a well-defined derivative at any point. They exhibit erratic behavior, and although they can be integrated (as integration measures the area under the curve), they defy differentiation in the conventional sense.
1. Weierstrass Function
The Weierstrass function is one of the first discovered examples of a continuous, nowhere differentiable function. It is defined as:
W(x) = ∑n=0∞ an cos(bn π x)
where:
- 0 < a < 1
- b is an odd integer such that ab > 1 + 3/2 π
This function is continuous but has no well-defined derivative at any point due to the rapid oscillations caused by the series.
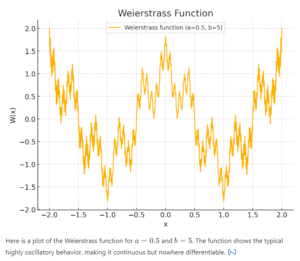
Integration: Yes, the Weierstrass function is integrable since it’s continuous and bounded. The integral of the function over an interval exists and is well-defined, but the result might not be simple to compute due to its complex structure.
2. Cantor Function (Devil’s Staircase)
The Cantor function is another famous example of a function that is continuous but nondifferentiable almost everywhere. It’s defined on the unit interval [0, 1] using the Cantor set and is constructed by removing the middle thirds repeatedly from each remaining segment.
Integration: The Cantor function is not differentiable almost everywhere, but it is integrable. In fact, the integral of the Cantor function over the interval [0, 1] is equal to 0.5.
3. Brownian Motion (Wiener Process)
A Brownian motion path, denoted B(t), is a random process that is continuous almost surely but is nowhere differentiable with probability 1. This is commonly used in fields such as physics and finance for modeling stochastic processes.
Integration: Brownian motion is integrable in a stochastic sense (stochastic integrals), and techniques such as Itô calculus are used to handle such integrals. However, this is a special kind of integration designed to handle the irregularities of stochastic processes.
Can They Be Integrated?
Yes, most nowhere differentiable functions can be integrated, especially in the Riemann or Lebesgue sense, because integration is concerned with measuring the “area under the curve,” while differentiation is focused on the local rate of change, which is what these functions lack.
For example:
- The Weierstrass function is integrable over any interval due to its continuity.
- The Cantor function is also integrable, though its derivative is 0 almost everywhere.
- For Brownian motion, special methods (stochastic integrals) allow for meaningful integration.
In general, continuity guarantees integrability, but differentiability is not necessary for a function to be integrable.