Derivation of de Broglie Wavelength 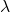\lambda

Start with the total energy of a de Broglie matter wave, combining rest mass and kinetic energy:

    \[ \frac{h v}{\lambda} = mc^2 + \frac{h^2}{2m \lambda^2} \]

Multiply both sides by \lambda^2 to eliminate denominators:

    \[ h v \lambda = mc^2 \lambda^2 + \frac{h^2}{2m} \]

Rewriting in standard quadratic form:

    \[ mc^2 \lambda^2 - h v \lambda + \frac{h^2}{2m} = 0 \]

This is a quadratic equation in \lambda, and we solve it using the quadratic formula:

    \[ \lambda = \frac{-(-h v) \pm \sqrt{(-h v)^2 - 4 \cdot mc^2 \cdot \frac{h^2}{2m}}}{2 mc^2} \]

Simplifying:

    \[ \lambda = \frac{h v \pm \sqrt{h^2 v^2 - 2 h^2 c^2}}{2 m c^2} \]

Or, factoring out constants:

    \[ \lambda(v) = \frac{h}{2mc^2} \left( v \pm \sqrt{v^2 - 2c^2} \right) \]

We choose the positive root to ensure that \lambda > 0:

    \[ \boxed{ \lambda(v) = \frac{h}{2mc^2} \left( v + \sqrt{v^2 - 2c^2} \right) } \]

 

Now, we have the wavelength in terms of the wave velocity. We can calculate the doppler shift.

    \[ \lambda(v) = \frac{h v + \sqrt{h^2 v^2 - 2 h^2 c^2}}{2 m c^2} \]

Factorizing out common terms:

(★)   \[ \lambda(v) = \frac{h}{2mc^2} \left( v + \sqrt{v^2 - 2c^2} \right) \]

To calculate the Doppler shift, we find the differential change in wavelength for a small change in velocity \Delta v:

    \[ \frac{d\lambda}{dv} = \frac{h}{2mc^2} \left( 1 + \frac{v}{\sqrt{v^2 - 2c^2}} \right) \]

Then the change in wavelength \Delta \lambda is approximately:

    \[ \Delta \lambda \approx \frac{d\lambda}{dv} \cdot \Delta v = \frac{h}{2mc^2} \left( 1 + \frac{v}{\sqrt{v^2 - 2c^2}} \right) \Delta v \]

Final Result — Doppler Shift of de Broglie Wavelength:

    \[ \boxed{ \Delta \lambda = \frac{h}{2mc^2} \left( 1 + \frac{v}{\sqrt{v^2 - 2c^2}} \right) \Delta v } \]