1️⃣ Lie Group → Lie Algebra: Example with 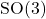\mathrm{SO}(3)

Step 1: Define the Lie group

\mathrm{SO}(3) = Special Orthogonal Group in 3D
Set of all 3 \times 3 real rotation matrices with:

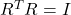  • R^T R = I (orthogonality)
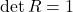  • \det R = 1 (special)

Step 2: Parametrize near identity

Take an element R(\theta) \approx I + \theta A + O(\theta^2), with small \theta.
A is in the tangent space — this defines the Lie algebra \mathfrak{so}(3).

Step 3: Compute Lie algebra

Plug R(\theta) into R^T R = I:

    \[ (I + \theta A^T)(I + \theta A) = I \Rightarrow A^T + A = 0 \]

Conclusion: A is antisymmetric 3 \times 3 matrix:

    \[ A = \begin{pmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{pmatrix} \]

The algebra \mathfrak{so}(3) is 3-dimensional, basis given by:

    \[ L_1 = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{pmatrix}, \quad L_2, \quad L_3 \]

Step 4: Lie bracket

The Lie bracket is matrix commutator:

    \[ [L_i, L_j] = \epsilon_{ijk} L_k \]

where \epsilon_{ijk} is the Levi-Civita symbol.

2️⃣ Affine Kac–Moody Algebra as a Generalization

Step 1: Start with finite Lie algebra \mathfrak{g}, e.g. \mathfrak{su}(2)

    \[ [J_i, J_j] = i \epsilon_{ijk} J_k \]

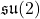
Step 2: Build loop algebra

Take functions of a circle S^1, parameterized by e^{int} (Fourier modes).
Now consider operators J_i(n), \; n \in \mathbb{Z}.

These satisfy:

    \[ [J_i(n), J_j(m)] = i \epsilon_{ijk} J_k(n + m) \]

Step 3: Add central extension

Introduce central charge k:

    \[ [J_i(n), J_j(m)] = i \epsilon_{ijk} J_k(n + m) + n \delta_{ij} \delta_{n + m, 0} k \]

Now the algebra is called an Affine Kac–Moody algebra \widehat{\mathfrak{su}(2)}.

Physical meaning:

  • Modes 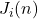J_i(n) generate local symmetry transformations along the loop (string or 1D system).
  • Central term 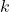k is related to quantum anomaly or level.

3️⃣ Example in Quantum Physics: WZW Model

Setup:

Fields g(z, \bar{z}) \in SU(N)
Action has Wess–Zumino term → topological term.

Resulting symmetry:

The model has left and right Affine Kac–Moody algebra symmetries:

    \[ \widehat{\mathfrak{su}(N)}_L \times \widehat{\mathfrak{su}(N)}_R \]

Operators J^a(z) (left currents) satisfy:

    \[ [J^a_n, J^b_m] = i f^{abc} J^c_{n + m} + n \delta^{ab} \delta_{n + m, 0} k \]

Similarly for right-moving sector.

Application:

  • String theory: Worldsheet theory of strings on group manifolds → governed by WZW models → governed by Kac–Moody algebra.
  • Conformal field theory: Classification of CFTs via Kac–Moody symmetries.
  • Statistical physics: 2D critical systems (spin chains, quantum Hall effect).

🧾 Conclusion

We’ve worked through:

  • Lie group 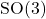\mathrm{SO}(3) → infinitesimal generators → Lie algebra \mathfrak{so}(3).
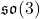  • Loop algebra of 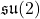\mathfrak{su}(2) → central extension → Affine Kac–Moody algebra \widehat{\mathfrak{su}(2)}.
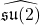  • WZW model → real-world quantum physics example of Kac–Moody symmetry.

Kac–Moody algebras provide the algebraic backbone for infinite-dimensional symmetry groups in modern quantum physics — essential in string theory, CFT, and 2D quantum systems.