Quantum Mechanics and the Transformation 1\(z-a)
Quantum Mechanics and the Transformation 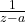
Transformations of the form ![]() , especially in the context of complex analysis, appear in quantum mechanics, particularly in the study of wave functions, scattering theory, and resonance phenomena. Here are some key examples:
, especially in the context of complex analysis, appear in quantum mechanics, particularly in the study of wave functions, scattering theory, and resonance phenomena. Here are some key examples:
1. Green’s Functions in Quantum Mechanics
In quantum mechanics, Green’s functions are used to solve differential equations related to the Schrödinger equation. The Green’s function for a Hamiltonian often involves terms like ![]() , where
, where ![]() is the energy of the particle and
is the energy of the particle and ![]() is the Hamiltonian operator.
is the Hamiltonian operator.
For a system with discrete energy levels, this can be represented as ![]() , where
, where ![]() is an eigenvalue (energy level) of
is an eigenvalue (energy level) of ![]() . This expression has a structure similar to
. This expression has a structure similar to ![]() and describes the response of a quantum system at specific energy levels.
and describes the response of a quantum system at specific energy levels.
2. Scattering Theory and the S-Matrix
In scattering theory, the S-matrix describes how incoming particles scatter off a potential. When studying scattering resonances, poles of the S-matrix in the complex energy plane become essential. These poles, often of the form ![]() , correspond to resonant states and can be analyzed using complex variables.
, correspond to resonant states and can be analyzed using complex variables.
This type of transformation reveals the positions of resonances, which are closely related to observable quantities like cross-sections in scattering experiments.
3. Complex Potentials and Resonances
In certain quantum mechanics problems, especially in nuclear and particle physics, complex potentials (like ![]() ) are introduced to represent interactions with a finite lifetime. These complex potentials allow the study of resonances and metastable states.
) are introduced to represent interactions with a finite lifetime. These complex potentials allow the study of resonances and metastable states.
Here, ![]() reflects how the resonance behaves near the complex energy value
reflects how the resonance behaves near the complex energy value ![]() . This is often visualized in the complex energy plane, where the imaginary part describes decay rates or lifetimes.
. This is often visualized in the complex energy plane, where the imaginary part describes decay rates or lifetimes.
4. Riemann Surfaces and Quantum Field Theory
In advanced topics like quantum field theory and string theory, transformations of complex variables such as ![]() are used to map solutions onto different parts of the complex plane. The study of Riemann surfaces and conformal mappings, where transformations like
are used to map solutions onto different parts of the complex plane. The study of Riemann surfaces and conformal mappings, where transformations like ![]() appear, help in defining fields and analyzing singularities in Feynman diagrams.
appear, help in defining fields and analyzing singularities in Feynman diagrams.
5. Analytic Continuation of Wavefunctions
Analytic continuation is a technique used in quantum mechanics for studying bound states and resonances by extending the energy variable into the complex plane. The transformation ![]() helps in understanding wavefunctions’ behavior as they approach singularities or branch points. This transformation is valuable in problems involving decaying states and quasi-bound states.
helps in understanding wavefunctions’ behavior as they approach singularities or branch points. This transformation is valuable in problems involving decaying states and quasi-bound states.
Summary
In each of these cases, the transformation ![]() helps capture specific behaviors, such as the response of a system near a resonance, the decay of metastable states, or the mapping of complex-valued functions in scattering theory. These applications emphasize the importance of complex transformations in both theoretical and practical aspects of quantum mechanics.
helps capture specific behaviors, such as the response of a system near a resonance, the decay of metastable states, or the mapping of complex-valued functions in scattering theory. These applications emphasize the importance of complex transformations in both theoretical and practical aspects of quantum mechanics.