Functions ONLY definable by their integrals – with applications
Functions ONLY Defined by Their Integrals
1. The Gamma Function 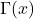
![]() , for
, for ![]() .
.
Applications:
- Generalization of factorials:
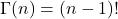 .
. - Used in probability distributions and statistical mechanics.
- Found in Feynman integrals in quantum physics.
2. The Beta Function 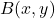
![]() .
.
Applications:
- Related to the Gamma function via
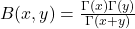 .
. - Used in Bayesian statistics and machine learning.
3. The Error Function 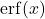
![]() .
.
Applications:
- Used in Gaussian probability distributions.
- Appears in heat and diffusion equations.
4. The Fresnel Integrals 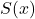 and
and 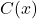
![]() ,
, ![]() .
.
Applications:
- Wave optics and diffraction patterns.
- Radar signal processing.
5. The Dirichlet Integral
![]() .
.
Applications:
- Fourier analysis and signal processing.
6. The Bessel Functions 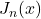
![]() .
.
Applications:
- Solutions to differential equations in cylindrical coordinates.
- Used in electromagnetics and fluid dynamics.
7. The Airy Function 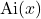
![]() .
.
Applications:
- Quantum mechanics and tunneling problems.
- Optics and wavefront analysis.
8. The Riemann Zeta Function 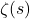
![]() , for
, for ![]() .
.
Applications:
- Number theory and prime distribution.
- Quantum field theory.
9. The Lambert W Function 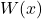
Defined by ![]() , with integral representation:
, with integral representation:
![]() .
.
Applications:
- Used in combinatorics and graph theory.
- Appears in quantum mechanics and delay differential equations.
10. The Polylogarithm Function 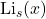
![]() .
.
Applications:
- Found in quantum field theory and statistical mechanics.
- Used in cryptography and information theory.