Finite Abelian Groups and Applications to Quantum Physics
Finite Abelian Groups and Applications to Quantum Physics
What Are Finite Abelian Groups?
A finite abelian group is a group ![]() with the following properties:
with the following properties:
- Closure: For any
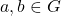 ,
, 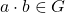 .
. - Associativity: For all
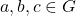 ,
, 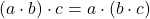 .
. - Identity: There exists an identity element
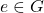 such that
such that 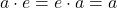 for all
for all 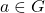 .
. - Inverses: For every
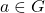 , there exists an
, there exists an 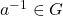 such that
such that 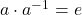 .
. - Commutativity: For all
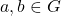 ,
, 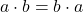 .
.
If the group has a finite number of elements, it is called finite.
Structure of Finite Abelian Groups
The Fundamental Theorem of Finite Abelian Groups states that every finite abelian group ![]() can be expressed as a direct product of cyclic groups of prime power order:
can be expressed as a direct product of cyclic groups of prime power order:
![]()
where ![]() are integers greater than 1.
are integers greater than 1.
Examples of Finite Abelian Groups
- Cyclic Groups:
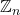 , the integers modulo
, the integers modulo 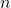 under addition.
under addition.- Example:
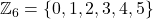 with addition modulo 6.
with addition modulo 6.
- Direct Product of Cyclic Groups:
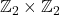 , the Klein four-group:
, the Klein four-group:
![Rendered by QuickLaTeX.com \[ \{(0, 0), (1, 0), (0, 1), (1, 1)\}. \]](https://stationarystates.com/wp-content/ql-cache/quicklatex.com-877e940e3b5f8564115d75c9ff3ecb9b_l3.png)
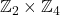 :
:
![Rendered by QuickLaTeX.com \[ \{(0, 0), (1, 0), (0, 1), (1, 1), (0, 2), (1, 2), (0, 3), (1, 3)\}. \]](https://stationarystates.com/wp-content/ql-cache/quicklatex.com-29c57973d9881284e822831e2cbf4539_l3.png)
- Additive Group of Finite Fields: The set of elements of a finite field
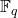 under addition forms a finite abelian group.
under addition forms a finite abelian group. - Root of Unity Groups: The
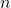 -th roots of unity
-th roots of unity 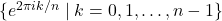 under multiplication.
under multiplication.
Applications to Quantum Physics
1. Quantum Mechanics and Symmetry
- Discrete Symmetries: Finite abelian groups often describe symmetries of quantum systems, such as the Klein four-group
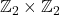 , which can describe symmetries in molecular structures or lattice vibrations.
, which can describe symmetries in molecular structures or lattice vibrations. - Conservation Laws: The symmetries of a system are associated with conserved quantities, often modeled using finite abelian groups.
2. Quantum Computing
- Quantum Gates: The structure of finite abelian groups is crucial in algorithms like Shor’s algorithm, where periodicity plays a significant role.
- Quantum Error Correction: Stabilizer codes, used in error correction, leverage abelian group structures to define subspaces.
3. Topological Phases of Matter
- Abelian Anyons: Quasiparticles in topological systems exhibit abelian statistics, modeled by finite abelian groups.
- Fractional Quantum Hall Effect: Finite abelian groups describe the ground state degeneracies and quasiparticle statistics of these systems.
4. Crystallography and Solid-State Physics
- Lattice Symmetries: Finite abelian groups classify vibrational modes (phonons) and electronic band structures.
- Bloch’s Theorem: Translational symmetry, often modeled as
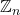 , leads to quantized energy levels in the form of Bloch waves.
, leads to quantized energy levels in the form of Bloch waves.
Conclusion
Finite abelian groups provide the mathematical foundation for understanding symmetry, periodicity, and conserved quantities in quantum systems. They play a crucial role in quantum computing, error correction, and the study of topological phases of matter, highlighting the deep connections between algebra and the physical world.