Examples of Taylor SEries versus Fourier Series
Intro
Which works better for a given function – a Taylor expansion or a Fourier Expansion? This post explores the pros and cons of each, using specific examples.
Examples of Taylor and Fourier Series Expansions
1. Polynomial Function: 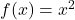
Taylor Series Expansion: ![]()
Fourier Series Expansion: ![]()
Best Fit: Taylor series
2. Trigonometric Function: 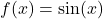
Taylor Series Expansion: ![]()
Fourier Series Expansion: ![]()
Best Fit: Fourier series
3. Exponential Function: 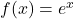
Taylor Series Expansion: ![]()
Fourier Series Expansion: Not practical
Best Fit: Taylor series
4. Piecewise Function: 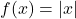 on
on ![Rendered by QuickLaTeX.com [-\pi, \pi]](https://stationarystates.com/wp-content/ql-cache/quicklatex.com-395b463e50a011903bd3425905d2abbc_l3.png)
Taylor Series Expansion: Not possible
Fourier Series Expansion: ![]()
Best Fit: Fourier series
5. Periodic Step Function: 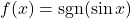
Taylor Series Expansion: Not possible
Fourier Series Expansion: ![]()
Best Fit: Fourier series
Comparison Table
| Function | Taylor Series | Fourier Series | Best Fit |
|---|---|---|---|
| Good (converges well) | Works if periodic but inefficient | Taylor series | |
| Good for small |
Best for periodic representation | Fourier series | |
| Excellent (globally convergent) | Poor (unless forced periodicity) | Taylor series | |
| Not possible | Works well (some Gibbs effect) | Fourier series | |
| Not possible | Best option (Gibbs phenomenon) | Fourier series |