Borel Algebras and Applications in Physics

Borel Algebra and Applications in Physics

Examples of Borel Algebras

Real Line ( $\mathbb{R}$ ):

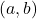The Borel algebra on $\mathbb{R}$ is generated by the open intervals $(a, b)$ . It includes:
- Open sets (e.g., $(0, 1)$ ).
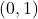- Closed sets (e.g., $[0, 1]$ ).
- Countable unions of open intervals (e.g., $\bigcup_{n=1}^\infty (a_n, b_n)$ ).
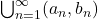- Countable intersections and complements of the above.
https://stationarystates.com/mathematical-physics/borel-algebras-and-applications-in-physics/
Euclidean Space ( $\mathbb{R}^n$ ):

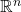The Borel algebra is generated by open subsets of 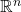$\mathbb{R}^n$ , such as open balls $\{ x \in \mathbb{R}^n : \|x - c\| < r \}$ .
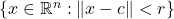Discrete Spaces:

For a finite or countable discrete space 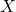$X$ , the Borel algebra is the power set of 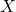$X$ , which includes all subsets of $X$ .
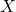Cantor Set:

The Borel algebra on the Cantor set includes all countable unions and intersections of basic “intervals” in the Cantor set.
Spheres and Compact Spaces:

For spaces like the 2-sphere 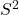$S^2$ , the Borel algebra includes all open and closed subsets of 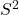$S^2$ and their countable unions, intersections, and complements.

Quantum Mechanics:
- Spectral Theory: The Borel algebra on 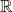$\mathbb{R}$ is used to define the spectral measure of self-adjoint operators, which assign probabilities to measurable subsets of eigenvalues.
- Measurement Theory: Quantum measurements are modeled as events in a Borel algebra, allowing probabilities to be defined via the Born rule.
Statistical Mechanics:
- Partition Functions: Borel measurable functions describe distributions over phase space or state space (e.g., Boltzmann distribution).
- Ergodic Theory: Dynamical systems often involve invariant measures defined on Borel algebras.
General Relativity:
- Causal Structure: Measurable subsets of spacetime manifolds, such as light cones, are defined using Borel algebras.
- Black Hole Thermodynamics: Borel measurable functions help define entropy and other thermodynamic properties of black holes.
Statistical Field Theory and Path Integrals:

The measure on the space of field configurations (or paths) is often constructed using Borel algebras, critical for defining and calculating Feynman path integrals.
Stochastic Processes in Physics:

Stochastic processes, such as Brownian motion or Langevin dynamics, use probability spaces underpinned by Borel algebras to define measurable events and random variables.