Derivation of GHZ using Dirac Notation
GHZ Derivation Using Dirac Notation
The GHZ state provides a clean, deterministic contradiction with local hidden variable theories using quantum mechanics and entangled states. Below is a step-by-step derivation using Dirac notation.
🔭 GHZ State
We define the canonical GHZ state for 3 qubits:
![]()
Each qubit is sent to one of three observers: Alice, Bob, and Charlie.
🧮 Measurement Operators
Each observer measures either:
- Pauli-X:
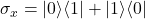
- Pauli-Y:
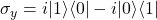
🔸 Example: 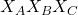
Applying ![]() to the GHZ state:
to the GHZ state:
![]()
So,
![]()
🔸 Example: 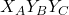
Apply ![]() to
to ![]() :
:
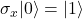 ,
, 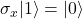
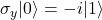 ,
, 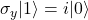
Operating on ![]() :
:
![]()
Operating on ![]() :
:
![]()
Thus:
![]()
But if we define the GHZ state with a minus sign:
![]()
Then:
![]()
✅ Eigenvalue: ![]()
🧾 Final Quantum Predictions
| Operator | Eigenvalue (Quantum) |
|---|---|
🤯 Local Realism Contradiction
Assume predefined values for each measurement (±1). Then, from the quantum predictions:
![]()
Multiply the last three:
![]()
Since squares of ±1 are 1, this implies:
![]()
This contradicts the earlier prediction:
![]()
❌ Logical Contradiction
Local hidden variable theories predict +1, quantum mechanics predicts −1. This contradiction is not statistical—it’s logical and deterministic.
✅ Thus, **local realism is incompatible with quantum mechanics**.
Leave a Reply