Mathematical Difference: Neutron Star vs Pulsar

Neutron Star

A neutron star is a highly dense remnant of a massive star after a supernova explosion. It is characterized by:

  • Mass: 1.4 M_\odot \leq M \leq 2.16 M_\odot
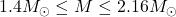
  • Radius: 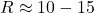R \approx 10-15 km
  • Density: 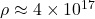\rho \approx 4 \times 10^{17} kg/m³
  • Escape velocity: v_e = \sqrt{\frac{2GM}{R}} \approx 0.4c

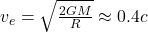
Pulsar

A pulsar is a type of neutron star that emits periodic electromagnetic radiation due to its rapid rotation and strong magnetic field. It follows additional mathematical constraints:

  • Rotation period: 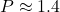P \approx 1.4 ms to a few seconds
  • Magnetic field strength: 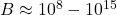B \approx 10^{8} - 10^{15} Gauss
  • Spin-down rate: 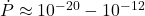\dot{P} \approx 10^{-20} - 10^{-12} s/s
  • Energy loss due to dipole radiation:
    L = \frac{2}{3} \frac{\mu^2 \omega^4}{c^3}

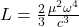
Key Difference

All pulsars are neutron stars, but not all neutron stars are pulsars. A neutron star becomes a pulsar if:

  • It has a strong enough magnetic field (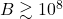B \gtrsim 10^{8} Gauss).
  • It rotates rapidly enough to emit detectable periodic signals.

Over time, pulsars lose energy and slow down, eventually becoming regular neutron stars.