Projection OPerators and Christoffel Symbols
Are Christoffel Symbols Related to Projection Operators?
This is a deep and fascinating question — and it’s insightful to sense a connection. While Christoffel symbols and projection operators arise in different mathematical settings (geometry vs. quantum mechanics), they both deal with how structures change or decompose in curved or constrained spaces.
🔧 Christoffel Symbols (Geometry)
- Appear in differential geometry.
- Encode how coordinate bases twist and turn in a curved manifold.
- Used to define the covariant derivative.
- Not tensors themselves, but help define how vectors change across space.
Formally:
![]()
🔬 Projection Operators (Quantum Mechanics)
- Act in Hilbert spaces, often infinite-dimensional vector spaces.
- A projection operator
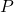 satisfies:
satisfies:
![Rendered by QuickLaTeX.com \[ P^2 = P, \quad P^\dagger = P \]](https://stationarystates.com/wp-content/ql-cache/quicklatex.com-e064b9e332bae69920c5c9a89e45a2fa_l3.png)
- Projects a vector onto a subspace (e.g., eigenstate space of an observable).
- Encodes measurement in quantum mechanics.
🌉 Conceptual Bridge
Both structures deal with components of vectors under constraints:
| Concept | Christoffel Symbols | Projection Operators |
|---|---|---|
| Setting | Curved space/manifold | Hilbert space |
| Purpose | Adjust derivative to follow curvature | Extract component in a subspace |
| Key Structure | Covariant derivative |
Operator |
| Acts On | Geometric vectors/tensors | Quantum states/vectors |
| Related To | Parallel transport, geodesics | Measurement, observables |
🧠 Deeper Similarity: Connections and Decompositions
– Christoffel symbols decompose how a vector changes: intrinsic vs. extrinsic parts.
– Projection operators decompose quantum states into subspaces.
Both are types of connections:
- In geometry: a connection tells you how to compare vectors at different points in space.
- In quantum theory: projections (and Berry connections) tell you how quantum states evolve in parameter space.
🌀 Advanced View: Gauge Theory Link
In modern physics:
- Christoffel symbols behave like gauge connections for gravity.
- Projection operators appear in Berry phase phenomena and in quantum gauge structures.
In both cases, we talk about how quantities transform when moving around in space or state space.
Connections define how things change when you move around in space (or Hilbert space), and curvature arises when this change depends on the path.
✅ TL;DR
They live in different worlds but share a core idea:
Both Christoffel symbols and projection operators are tools for tracking and constraining change under structure — whether it’s spatial curvature or Hilbert space decomposition.