Constructing a wave that is spiked in just one small region is not easy.

When you superpose several waves, you have to do so in a way that they constructively interfere only in this small region and are essentially destructively interfering everywhere else.

 

Complex Plane Wave Evolution

Wave Description

A plane complex harmonic wave can be described by the function:

ψ(x,t) = A ei(kx – ωt)

where:

  • A is the amplitude
  • k is the wave number
  • ω is the angular frequency
  • x is the spatial coordinate
  • t is time

(a) Evolution in Time

At t = 0, the wave is:

ψ(x,0) = A ei kx

As time progresses, the phase evolves as:

ψ(x,t) = A ei(kx – ωt)

The factor e-i ω t represents a time-dependent oscillation at frequency ω.

(b) Evolution in Space (along x)

At a fixed time t, the wave is:

ψ(x,t) = A ei(kx – ωt)

The term ei kx represents a spatial oscillation with wavenumber k, meaning the wave has a wavelength:

λ = 2π/k

The phase velocity is:

vp = ω/k

The entire waveform shifts in space over time at this velocity.

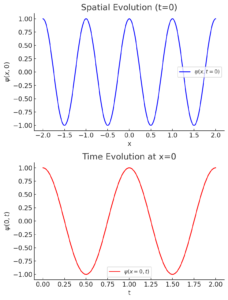
Graphical Representation

The following graphs illustrate the evolution of the plane wave:

  • Spatial Evolution: Wave as a function of x at t = 0.
  • Time Evolution: Oscillation at a fixed spatial point (e.g., x = 0).
complex plane wave evolution
complex plane wave evolution