📘 Summary of the Paper

In this pioneering paper, P.A.M. Dirac explores the mathematical and physical advantages of using
complex variables in quantum mechanics. Traditional quantum theory relies on wave functions
over real-valued observables (like position q or momentum p). Dirac proposes extending momentum
p into the complex plane, gaining powerful tools from complex analysis—such as
analytic continuation, contour integration, and pole residues.

The key contribution is a “fundamental theorem” about integrals in quantum mechanics: if the integrand
consists of two functions regular (analytic) in complementary half-planes, one can deform the real axis
into a complex contour that avoids singularities without changing the value of the integral.
This idea is applied to wave function representations and operator matrix elements in momentum space.

Dirac applies the theory to familiar problems, notably the hydrogen atom, reformulating
Schrödinger’s solution using this complex variable formalism. This new formulation simplifies
computations and gives deeper insight into boundary conditions, regularity at infinity,
and the origin of quantization.

🔢 Detailed Mathematical Explanations

1. Fourier Representation and Complex Momentum

Dirac starts by moving from position q to momentum p space:

\

    \[ \psi(p) = \langle p | \psi \rangle = \frac{1}{\sqrt{2\pi\hbar}} \int_0^\infty e^{-ipq/\hbar} \psi(q)\,dq \\]

Unlike standard theory where p \in \mathbb{R}, Dirac now allows p \in \mathbb{C}.
If \psi(q) is bounded and vanishes as q \to \infty, then \psi(p) is analytic in
the lower half-plane (Imp < 0) and can be analytically continued across the real axis.

2. Dirac’s Fundamental Theorem

In an integral of the form:

\

    \[ \int_{-\infty}^{\infty} \langle A | p \rangle \langle p | B \rangle \, dp \\]

If:

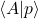  • \langle A | p \rangle is analytic in the upper half-plane
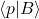  • \langle p | B \rangle is analytic in the lower half-plane

then the path of integration can be deformed into the complex plane to avoid poles.

For a simple pole at p = a:

\

    \[ \langle p | B \rangle \sim \frac{1}{p - a\hbar} \Rightarrow \psi(q) \sim e^{iaq/\hbar} \\]

The contour is then deformed below the pole, consistent with standard quantum interpretations.

3. Conditions at Infinity

If the Laurent expansion of \langle p | \psi \rangle has a constant term:

\

    \[ \langle p | \psi \rangle = a_0 + \frac{a_1}{p} + \cdots \\]

This implies a delta function in position space:

\

    \[ \psi(q) = a_0 \delta(q) \\]

To maintain finite integrals and valid inner products, integration contours must
avoid infinity in the appropriate direction. This leads to a generalization of the
fundamental theorem: if a constant term appears in one factor, the contour must encircle
infinity in the opposite half-plane.

4. Operators in Complex Momentum Space

  • Identity operator:
    \

        \[ I = \frac{1}{2\pi i} \int \frac{1}{p' - p} |p' \rangle \langle p'| \, dp' \\]

  • Momentum operator:
    \

        \[ \langle p' | \hat{p} | p'' \rangle = \frac{-i\hbar p'}{2\pi(p' - p'')} \\]

  • Position operator:
    \

        \[ \langle p' | \hat{q} | p'' \rangle = i\hbar \frac{\partial}{\partial p'} \delta(p' - p'') \\]

  • Inverse position operator:
    \

        \[ \langle p' | \hat{q}^{-1} | p'' \rangle = -\frac{1}{\hbar} \log(p' - p'') \\]

5. Application to the Hydrogen Atom

Radial Schrödinger equation in position space:

\

    \[ \left[ -\frac{\hbar^2}{2m} \left( \frac{d^2}{dq^2} - \frac{n(n+1)}{q^2} \right) - \frac{e^2}{q} \right] \psi(q) = W \psi(q) \\]

is transformed into p-representation:

\

    \[ \left[ -p^2 + 2(a+1) \frac{1}{p} + 2mW - \frac{2ime^2}{\hbar} \hat{q}^{-1} \right] \psi(p) = 0 \\]

Choosing asymptotic behavior:
\

    \[ \psi(p) \sim p^\alpha \Rightarrow \text{Take } \alpha = -1 \text{ to ensure decay at } \infty \\]

Quantization arises from requiring regularity at poles:
\

    \[ \frac{me^2/\hbar}{\sqrt{-2mW}} = s \in \mathbb{Z}^+ \Rightarrow \text{Bohr energy levels} \\]

✅ Key Takeaways

  • Extending 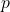p to complex values enables analytic tools in QM.
  • Integration contours can be deformed to bypass singularities safely.
  • Singularities at infinity are handled analogously to real poles.
  • Operators acquire elegant matrix forms using complex functions.
  • Hydrogen atom solutions are simplified in this formalism.