Gleason’s theorem with examples
Gleason’s Theorem Explained Using Single-Particle and Two-Particle Systems
Read this post on Projection Operators first.
1. What Is Gleason’s Theorem?
Gleason’s theorem states that in a Hilbert space of dimension ![]() , the only valid probability measure for quantum measurements must follow the Born rule:
, the only valid probability measure for quantum measurements must follow the Born rule:
![]()
where:
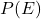 is the probability of measuring outcome
is the probability of measuring outcome 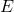 .
.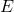 is a **projection operator** representing a measurement.
is a **projection operator** representing a measurement.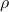 is the **density matrix** of the quantum state.
is the **density matrix** of the quantum state.
2. Single-Particle Spin Measurement
Consider a spin-![]() particle (like an electron) measured along the
particle (like an electron) measured along the ![]() -axis.
-axis.
Spin Observable 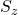
The spin operator is:
![]()
The possible measured values (eigenvalues) are:
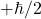 (Spin up,
(Spin up, 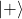 )
)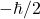 (Spin down,
(Spin down, 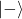 )
)
Projection Operators
Each measurement outcome corresponds to a projection operator:
![]()
![]()
Measurement Probabilities
If the quantum state is ![]() , the measurement probabilities are:
, the measurement probabilities are:
![]()
![]()
Single-Particle Measurement Diagram
Spin Measurement Device (Stern-Gerlach)
|
↑ ( +ℏ/2 ) | ↓ ( -ℏ/2 )
--------------------->--------------------
|ψ⟩ = α|+⟩ + β|−⟩
3. Two-Particle Entangled State
Consider two spin-![]() particles in the Bell state:
particles in the Bell state:
![]()
Observable: Total Spin Along  -Axis
-Axis
The total spin operator is:
![]()
The possible measured values are:
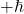 (both particles spin up)
(both particles spin up)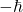 (both particles spin down)
(both particles spin down)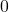 (one up, one down)
(one up, one down)
Measurement Probabilities
For the Bell state ![]() , Gleason’s theorem ensures that the measurement outcomes must obey:
, Gleason’s theorem ensures that the measurement outcomes must obey:
![]()
![]()
![]()
Entanglement Measurement Diagram
Particle A Particle B
----------- -----------
| +⟩ -⟩ | | +⟩ -⟩ |
------------------ ------------------
| Bell State: |Φ+⟩ = 1/√2 (|+⟩|+⟩ + |−⟩|−⟩)
|
| If A is measured as +ℏ/2, then B must be +ℏ/2.
| If A is measured as -ℏ/2, then B must be -ℏ/2.
4. Conclusion
- Gleason’s theorem proves that quantum measurement probabilities must follow the Born rule.
- Any attempt to assign classical probabilities to measurement outcomes contradicts the additivity condition.
- This rules out non-contextual hidden-variable theories and reinforces the fundamental role of quantum uncertainty.