Complex fourier transform and Wave Packets
Constructing a wave that is spiked in just one small region is not easy.
When you superpose several waves, you have to do so in a way that they constructively interfere only in this small region and are essentially destructively interfering everywhere else.
Complex Plane Wave Evolution
Wave Description
A plane complex harmonic wave can be described by the function:
where:
- A is the amplitude
- k is the wave number
- ω is the angular frequency
- x is the spatial coordinate
- t is time
(a) Evolution in Time
At t = 0, the wave is:
As time progresses, the phase evolves as:
The factor e-i ω t represents a time-dependent oscillation at frequency ω.
(b) Evolution in Space (along x)
At a fixed time t, the wave is:
The term ei kx represents a spatial oscillation with wavenumber k, meaning the wave has a wavelength:
The phase velocity is:
The entire waveform shifts in space over time at this velocity.
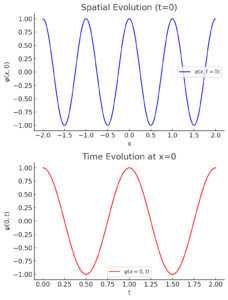
Graphical Representation
The following graphs illustrate the evolution of the plane wave:
- Spatial Evolution: Wave as a function of x at t = 0.
- Time Evolution: Oscillation at a fixed spatial point (e.g., x = 0).